راه حل های آزمون عملی یک

سلام!

خب بدون مقدمه می‌ریم سراغ جواب سوال ها:

سوال ۱ :‌

بلاک های ماکسیمال صندلی ها را در نظر بگیرید که همزمان شامل معلم و دانش آموز نباشند. در بلاک های اول و آخر همه می‌توانند پاپ کرن بخورند ولی در بلاک های وسطی دقیقا یک نفر نمی‌تواند. پس اگر تعداد بلاک های وسطی را x بگیریم جواب سوال n-x میشه.

سوال ۲ :

فرض کنید dp i,rev رو تعریف می‌کنیم مینیمم تعداد حرکات لازم اگر که بخوایم i تا حرف اول رشته رو تبدیل به A کنیم. و rev هم می تونه 0 یا 1 باشه که بهمون میگه قبل از شروع کار ما i تای اول برعکس شده‌اند یا نه.

حالا توجه کنید که اگر تصمیم بگیریم یک حرکت بزاریم که فقط i رو عوض کنه اونوقت مستقل از اینکه خونه i ام چی هست می تونیم فرض کنیم که در آخر می‌تونیم به A تبدیلش کنیم. اگر هم تصمیم بگیریم که تکی i رو عوض نکنیم دو حالت داریم. یا خونه i ام الان برابر با A هست که در اینصورت نباید کاری انجام بدیم. یا اینکه برابر نیست که باید با یک حرکت i تای اول رو عوض کنیم.

فرض کتید change متغیری بولین باشد که نشان می دهد بعد از اعمال rev باز هم باید خانه i ام را تغییر دهیم یا نه.

dp i,rev = min( 1 + dp i-1,rev ,  change + dp i-1,rev ^ change )

سوال ۳ :

لم : یک عدد بر ۱۱ بخش پذیر است اگر و فقط اگر یکی در میان رقم هایش را جمع و منها کنیم و حاصل بر ۱۱ بخش پذیر باشد!

اثبات :

a1a2a3...an = a1 * 10 ^ (n-1) + a2 * 10 ^ (n-2) + ... + an = a1 * -1 ^ (n-1) + a2 * -1 ^ (n-2) + ... + an    (mod 11)

که حکم را ثابت می‌کند.

حالا واضحه که عدد m همیشه بر ۱۱ بخش پذیر خواهد بود. پس کافیه برای عوامل اول ۲ و ۳ و ۵ و ۷ و ۱۱ چک کنیم که آیا m بر اون ها بخش پذیر هست یا نه.

فرض کنید می‌خواهیم باقی مانده m  را بر p پیدا کنیم. برای اینکار هم می توانیم از پرارزش ترین رقم شروع کنیم و در هر مرحله باقی مانده تقسیم i رقم اول بر p  را حساب کنیم. اگر این باقی مانده تا الان r باشد و رقم i+1 ام x باشد داریم :

r = ( r * 10 + x ) % p

سوال ۴ :

اول از همه اینکه فاصله منهتنی دو نقطه x1,y1 و x2,y2 برابر با |x1-x2| + |y1-y2| هست. می بینیم که ابعاد x و y با هم هیچ ارتباطی ندارند پس می توان آنها را جدا جدا حل کرد و سپس جواب های به دست آمده را با هم جمع کنیم و خروجی بدیم.

حالا بررسی کنید که اگر x ما یک واحد زیاد شود جواب چه تغییری می کند. فاصله ما از نقاطی که x کمتر مساوی دارند یک واحد زیاد می شود و از نقاطی که x بیشتر دارند یک واحد کم می شود. مشابها حالتی که x یک واحد کم شود هم قابل بررسی است.

پس اگر بتوانیم در هر مرحله تعداد نقاطی که مختصات x کمتر مساوی از x ارشیا دارند را حساب کنیم می توانیم با این اطلاعات تغییرات جواب را حساب کرده و جواب جدید  را به دست بیاوریم. برای این کار کافیه کل x ها را در یک آ رایه سورت شده ذخیره کنیم و با باینری سرچ ( یا تابع lower_bound ) این تعداد را پیدا کنیم.

سوال ۵ :

برای حل این سوال راه حل های متفاوتی وجود داشت از جمله راه هایی با استفاده از ایده هایی مثل sqrt یا centroid.

اما در اینجا راه حلی دیگر را بیان می‌کنیم که احتمالا ایده کلی آن برای شما جدید و جالب و قابل تعمیم است!

سوال معادل این است که یک درخت n راسی وزن دار داریم و q تا کوئری که در هر کدام دو مجموعه نه لزوما مجزا از رئوس به نام های A و B داده می‌شود و  هدف پیدا کردن کوتاه ترین مسیری است که یک سر عضو A و سر دیگر عضو B باشد.

ابتدا در نظر بگیرید که می توانیم هر کوئری را O(n) جواب بدهیم. کافیست با یک bfs مینیمم فاصله هر راس از یک راس مجموعه A را به دست بیاوریم و جواب مینیمم این فاصله ها در بین رئوس B خواهد بود.

اجتماع مجموعه های A و B را S بنامید. حالا توجه کنید که برای بسیاری از رئوس به دست آوردن این مقدار لازم نیست! پس هدف ما است که یک درخت کوچکتر بسازیم که در آن به ازای هر راس S راسی معادل  وجود داشته باشد و فاصله هر دو راس در S برابر با فواصل معادل های آنها در درخت جایگزین باشد!

لم : اگر مچموعه S از راس های درخت را داشته باشیم که t عضو دارد می توانیم حداکثر t-1  راس به آن اضافه کنیم که مجموعه جدید نسبت به عمل Lca بسته باشد. (به عبارتی Lca هر دو راس مجموعه عضو مجموعه باشد.‌ )

اثبات :

کافیست رئوس را بر حسب استارتینگ تایم صعودی سورت کنید. سپس به ازای هر دو راس متوالی در S مثل a,b ما Lca(a,b) را به مجموعه اضافه می‌کنیم. ( پس حداکثر t-1 عضو اضافه کردیم )

حالا دوباره راس ها را بر حسب استارتینگ تایم صعودی سورت کنید و اگر a,b دو راس متوالی باشند پدر b همان Lca(a,b) خواهد بود! (باید وزن یال بین a,b باید طول مسیر بین a,b در درخت اصلی باشد)

پس به ازای مجموعه S از راس ها می توان درخت جدیدی با تعداد رئوس حداکثر 2 * |S| ساخت و همانطور که در ابتدا کوئری  را O(n) جواب دادیم می توان در درخت جدید کوئری را O(|S|) حل کرد!

سوال ۶ ؛

حل کامل سوال در اینجا گفته نمی‌شود. بعد از فهمیدن هینت زیر انقدر به سوال فکر کنید تا حل بشه! 😃

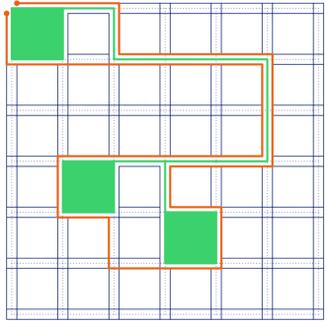
اول از همه اینکه دایسترا بزنید و بعد از داخل درخت دایسترا از گوشه بالا چپ جدول به گوشه بالا چپ همه روستا هایی که باید دورشون دیوار بکشیم یک مسیر بکشید. ( با رنگ سبز در شکل زیر مشخص شده. )

حالا مسئله معادل پیدا کردن یک دور شامل گوشه بالا سمت چپ جدول هست به طوریکه مسیر سبز که کشیدیم را قطع نکند. ( دور با رنگ نارنجی مشخص شده )

خب امیدوارم که از سوال ها خوشتون اومده باشه.

اگه چیزی رو نفهمیدید یا اشتباه گفتم توی کامنت ها بگید.  به زودی هم با یه سری سورپرایز بر می‌گردیم. :))

نویسنده : شایان پردیس